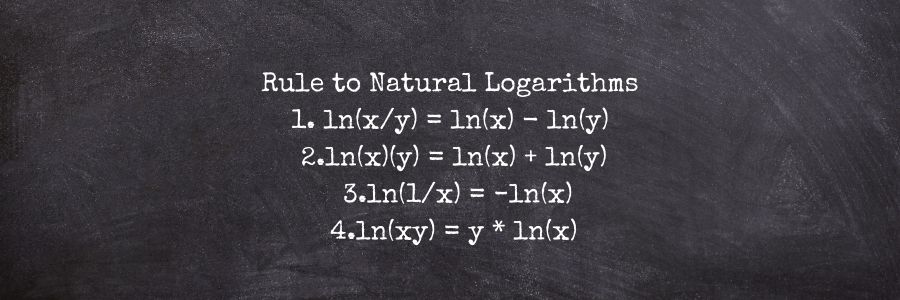Natural Log Rules with e

Natural Log Rules with e: You’ll likely cover natural logs if you’re taking a high school or college math class. This means that you will have to understand what are natural logs.

Although Natural logs may seem tough to most students, they are easily solved once you comprehend the key rule to natural logs. To help you understand better we have looked at the important natural logarithm rule. In addition, we have also discussed other natural log properties and given several examples to give you a better understanding.

What Is a natural logarithm?

The natural log is the logarithm to the base of the number e. It is the inverse function of an exponential function. They are special types of logarithms and are used in solving time and growth problems

In simple mathematics terms, a natural log is a log to the base _e i.e. Log_e. It can also be written in another form of ln. For example

Log_e 40 can also be written as ln40

ln 40 =6.3888795

The letter ‘e’ symbolizes a mathematical constant also known as the natural exponent. It has a set value of 2.71828.

e = 2.71828.

Read Also: List of Extracurricular activities

 

ln Rules or Natural Log Rules 

Below are the Key Rule to Natural Logarithms

1. Quotient Rule

ln(x/y) = ln(x) – ln(y)

The natural logarithm of the division of x and y is the difference of the ln of x and ln of y.

Example: ln(9/4) = ln(9) – ln(4)

2. Product Rule

ln(x)(y) = ln(x) + ln(y)

The natural logarithm of the multiplication of x and y is the sum of the ln of x and ln of y.

Example: ln (8)(8) = ln(8) + ln(8)

3. Reciprocal Rule

ln(1/x) = −ln(x)

The natural logarithm of the reciprocal of x is the opposite of the ln of x.

Example: ln(⅓)= -ln(3)

4. Power Rule

ln(xy) = y * ln(x)

The natural logarithm of x raised to the power of y is y times the ln of x.

Example: ln(62) = 2 * ln(6)

Read Also: Transition Sentences for Essays

Natural Log Rules with e

1. Natural log of any negative number is undefined i.e. Loge – 40 or ln (– 40) is undefined
2. Natural log of zero is undefined i.e. Loge 0 or ln (0) is undefined

NB: When using a calculator for the above two, you will get a notice for math error

3. Natural log of 1 is zero i.e. Loge 1 or ln (1) is zero
4. Natural log of infinity is infinity i.e. ln (∞)= ∞
5. The natural log of e is one i.e. ln (e) is 1
6. The natural log of e raised to power x is x i.e. ln(e^x) = x ( example ln(e⁶) =6)
7. e raised to the ln power i.e e^ln(x) =x (example e ^{ln (2)} =2)

How to Calculate Natural Log

Example 1

Evaluate ln(5²/3)

First, we use the quotient rule to get: ln(5²) – ln(3).

Next, we use the power rule to get: 2ln(5) -ln(5).

If you don’t have a calculator, you can leave the equation like this, or you can calculate the natural log values: 2(1.6094) – 1.6094 = 3.2188- 1.6094 = 1.6094

Example 2

Solve ln (5x-6) =2

Every time you have many variables within the natural log (ln) brackets like in the above case, you should make e the base and everything else the exponent of e. At that point you’ll get ln and e next to each other and, as we know from the natural log rules, e^ln(x)=x.

So, the equation becomes e^ln(5x-6)=e2

Since e^ln(x)=x, e^ln(5x-6)= 5x-6

Therefore 5x-6= e²

As e is a constant, you can then calculate the value of e2, either by using the e key on your calculator or using e’s estimated value of 2.718.

5x-6 = (2.718²)=7.389

Now we’d add 6 to both sides

5x-6 +6= 7.389+6

5x= 13.389

X=13.389=

5

X=2.6778

Example 3

Simplify: 6 ln_e(y) + 2ln_e(4y)-ln_e(8y⁶)

6 ln_e(y) + 2ln_e(4y)-ln_e(8y⁶)

=ln_e(y⁶) + ln_e(4y)²-ln_e(8y⁶)

=ln_e(y⁶. 16y²)-ln_e(8y⁶)

=ln_e(16y⁸)-ln_e(8y⁶)

=ln_e(16y⁸)

8y⁶

=lne(2y²)

Conclusion: Natural Log Rules with e

Natural logarithms are easy to tackle once you understand their basic rules. Take your time to fully comprehend what each rule means. In addition, try as many examples as possible. Eventually, you will like the topic and be able to solve all the questions coming your way.